Why is Vibration Amplitude in G?

Those looking for the Quick Vibe Estimator will find the tool in AB-031: Vibration Motor Calculators – ERMs and LRAs

Our vibration motors and linear resonant actuators use the unit G to describe their vibration amplitude. It leaves some of our customers with the question exactly what is G?

Well, 1 G is equal to the acceleration from gravity:

$$1G = 9.8 \frac{m}{s^{2}}$$

What we feel as vibrations are simply the object being repeatedly displaced and a very high frequency. But why do we express the vibration amplitude as acceleration (G) instead of a force (N) or the displacement (mm)?

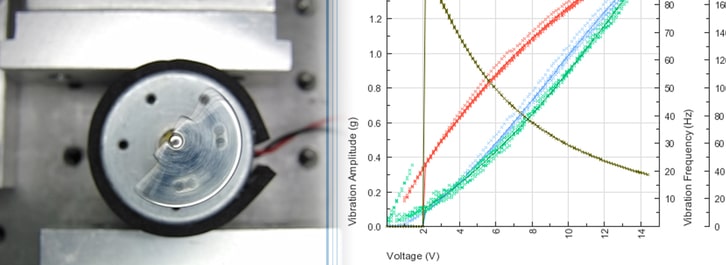
Those looking for the Quick Vibe Estimator will find the tool in AB-031: Vibration Motor Calculators – ERMs and LRAs

Our vibration motors and linear resonant actuators use the unit G to describe their vibration amplitude. It leaves some of our customers with the question exactly what is G?

Well, 1 G is equal to the acceleration from gravity:

$$1G = 9.8 \frac{m}{s^{2}}$$

What we feel as vibrations are simply the object being repeatedly displaced and a very high frequency. But why do we express the vibration amplitude as acceleration (G) instead of a force (N) or the displacement (mm)?

Why not use Displacement (mm) or Force (N)?

Vibration motors are not used on their own – they’re attached to a product/device/piece of equipment that is intended to vibrate. Therefore we are interested in the whole system (motor + target mass).

We measure the vibration amplitude by mounting the motor on a known target mass and reading the results from an accelerometer. This helps us plot our Typical Performance Characteristics graph.

The force of a vibration motor is governed by the equation:

$$F = m \times r \times \omega ^{2}$$

Where \(F\) is the force, \(m\) is the mass of the eccentric mass on the motor (not the whole system), \(r\) is the eccentricity of the eccentric mass, and \( \omega \) is the frequency.

We can see that the vibration force of the motor doesn’t take the target mass into consideration. As you can imagine, a much heavier object would require more force to generate the same acceleration as a small and light object. This means when using the same motor on the two objects, the vibration amplitude would feel much smaller in the heavy object – even though the motor has the same force.

Another aspect of the motor is the vibration frequency:

$$ f = \frac{Motor \: Speed \:(RPM)}{60}$$

The displacement is directly affected by the vibration frequency. Due to the cyclical nature of vibration devices, for every force acting upon the system, there is eventually an equal and opposite force. With high-frequency vibrations, the time between the opposing forces is reduced, which means the system has less time to be displaced. In addition (similar to the force above) heavier objects are displaced less with the same force.

If you ‘Normalise’ G, what about Force or Displacement?

It’s true, we provide a Typical Normalised Vibration Amplitude. This means our acceleration measurements are adjusted to reflect the resulting vibration amplitude for a 100g mass (it makes for easy comparison between different models). We could calculate normalised ratings for force and displacement, including the rated frequency.

However as our test systems measure acceleration (G) and it requires additional calculations to provide either the normalised force (N) or the normalised displacement (mm), it makes the most sense to use G.

For quick calculations, or to demonstrate the above, use the Quick Vib Estimator. Try entering random information to start, then try these tests:

• What values are affected by Target Mass?
• Can you adjust the Vibration Displacement without affecting the Vibration Force or Acceleration?
• What value affects all three resulting measurements?

---