Reading the Motor Constants from Typical Performance Characteristics

DC motor constants can be a confusing world, there’s a lot of differing information and relationships can be difficult to figure out due to inconsistent naming and units.

You shouldn’t need to find the constants for our vibration motors, they already have a fixed load and all the pertinent information like vibration amplitude and frequency is available on the datasheets you can download from our Product Catalogue. However, you may want to know the constants for our DC motors and DC gearmotors.

We will do our best to clarify as many of the different names as possible below. We will also use the SI units – something that is missing from a lot of guides.

Torque Constant \(k_{t}\)

AKA: “Motor constant”

SI Units: \( \frac{Nm}{A}\)

Relationship: Torque over Current

Value: holds the same value as the motor voltage constant, \(k_{e}\), below. That is \(k_{t} = k_{e}\).

Motor Voltage Constant, \(k_{e}\)

AKA: “electic constant” , “counter emf equation constant” , “back-emf constant” ,  \(k_{b}\)

SI Units: \( \frac{V}{rads^{-1}}\)   (or voltage over radians per second)

Relationship: Voltage over Speed

Value: holds the same value as the torque constant, \(k_{t}\), above. That is \(k_{e} = k_{t}\).

Speed Constant, \(k_{s}\)

AKA: “Speed equation constant”

SI Units: \( \frac{rads^{-1}}{V}\) (or radians per second over voltage)

Relationship: Speed over Voltage

Value: the inverse of the motor voltage constant, i.e. \(k_{s} = \frac{1}{k_{e}} = \frac {1}{k_{t}} \)

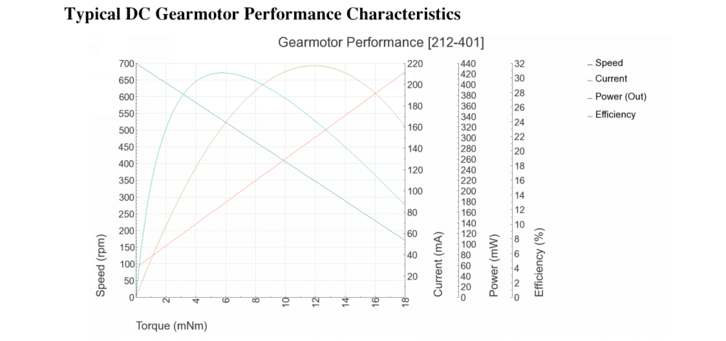
You can read or calculate the above constants from our datasheets. It is important to remember the above relationships are based on ideal motors, and do not take losses such as friction into account. Therefore there may be some variation in your resulting figures.

To calculate the Torque Constant read the current draw at a given torque on the Typical Performance Characteristics graph. Now divide the torque by the current.

To calculate the Motor Voltage Constant read the no-load speed (rpm) and convert it to radians per second. Take the Rated Voltage of the motor and divide it by the speed.

To calculate the Speed Constant read the no-load speed (rpm) and convert it to radians per second. Divide this number by the Rated Voltage.

Be sure to convert all your readings to the correct units before making the calculations, especially speed (RPM -> radians per second). If for some reason you can’t calculate the constant you need, remember the relationships

For brushed DC motors and SI units: \( k_{t}(\frac{Nm}{A}) = k_{e}(\frac{V}{rads^{-1}})=k_{s}(\frac{rads^{-1}}{V}) \)

---