Why Does the Resonant Frequency of an LRA Shift?
Linear resonant actuators must be driven with an AC signal at their resonant frequency, it only takes a couple of Hz in either direction for the vibration strength to dramatically decrease. To make driving LRAs even more challenging, the resonant frequency can shift.
What Causes the Shift
The equivalent circuit of the LRA contains an electrical section and a mechanical section. First, the resistance and the inductance of the internal coils are modelled by a resistor (R_{1}) and inductor (L_{1}).
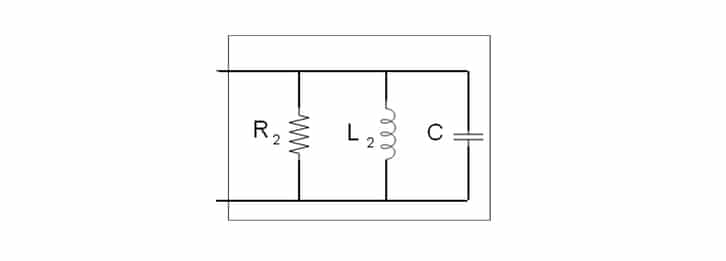
The biggest influence on the resonant frequency shifting is the mechanical equivalent circuit. The LRA’s design is very similar to a loudspeaker, and we can see this with the parallel RLC circuit (that’s a resistor, an inductor, and a capacitor in parallel).
You don’t need to understand the exact workings of the RLC section to understand why the resonant frequency shifts, but if you want to you can read about it all in Application Bulletin 020: Understanding Linear Resonant Actuators.
Resonance occurs when the impedance of the RLC circuit is at a maximum. The impedance of a capacitor and inductor both vary with the frequency of the electrical input:
$$Z_{C} = \frac{1}{j \omega C}$$
$$Z_{L} = j \omega L$$
As the frequency increases the capacitor’s impedance decreases, but the inductor’s increases. There is, therefore, a particular frequency that will balance these two impedances to give the maximum overall impedance. This is the resonant frequency, which we can see is also dependant upon the values ( C ) and ( L ).
Remember, this is an equivalent circuit for the mechanical model of the LRA. We are therefore using electrical components to simulate real-life mechanical factors. For example, a change in the stiffness of the internal spring can be represented by a change in the values of the resistor (R_{2}), inductor (L_{2}), or capacitor (C).
This means when the “real life” mechanical world changes, the resonant frequency will shift due to the change in impedance. Here are some examples that could cause a shift in resonant frequency:
Normal tolerances from the manufacturing process
Age of component (stiffness of spring)
LRA orientation (requires extra force to overcome gravity)
Extreme temperatures
Mounting (soft vs hard materials, e.g. skin vs PCB)
Some factors will have a bigger impact than others, but one of the most challenging aspects is that the level of shift is usually unknown.
The Solution
Thankfully there are techniques to measure the resonant frequency. This is not achieved by calculating the changes in the mechanical environment, instead, it is measured electrically.
The easiest solution is to use an LRA driver that has an auto-resonance feature built-in. This is the approach that we have taken with our upcoming haptic feedback evaluation kit.

Get in touch
Speak to a member of our team.
Motor catalogue
Looking for our products?
Reliable, cost-effective miniature mechanisms and motors that meet your application demands.
Discover more
Resources and guides
Discover our product application notes, design guides, news and case studies.
Case studies
Explore our collection of case studies, examples of our products in a range of applications.
Precision Microdrives
Whether you need a motor component, or a fully validated and tested complex mechanism – we’re here to help. Find out more about our company.