Torque Calculations for Gearmotor Applications

Given a lever, Archimedes may have been able to move the Earth, but given one of our DC motors just what can you lift?

Torque is a force around a given point, applied at some distance from that point. In other words, it is a measure of how much a force causes an object to rotate.

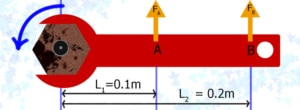
Let’s imagine we have a bolt that has rusted in place and requires a torque of 3Nm before it’ll budge. Intuitively we know that it is easier to turn the nut if we push the spanner at B rather than at A because the distance \(L_{1}\) is greater than \(L_{2}\). But how much easier?

If we apply a force \(F\) at a right angle to the spanner at a distance \(L\), we can figure out the torque (\(\tau\)) using:

$$\tau = F \times L$$ Equation 1

As \(L_{2} = 2 \times l_{1}\), the turning force on the bolt is twice as great. So to turn our rusted bolt we’ll need to apply 30N at point A, or just 15N is we apply force at point B.

But how does this help us figure out what weight our motors can lift?

Firstly, if you want to lift something with a motor you’ll want to make a pulley wheel and fit it over the end of your motor. Then tie a string to your object, and wrap it around the pulley: something like this:

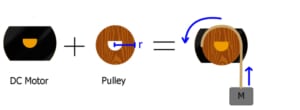
We have two variables in the system. One is the radius of the pulley ‘r’, and the other is the size of the mass. From this, we can calculate the torque exerted by the mass (a torque which our gearmotor must be able to exceed in order to lift the mass).

Alternatively, if we have already selected our gearmotor, it becomes a case of re-arranging the torque equation to find out either the maximum load, the motor can lift or the radius for the pulley. For our spanner, we showed that

$$ \tau = F \times L $$ Equation 1

In the case of our pulley,  the force exerted is due to the mass being accelerated by gravity:

$$ \tau =(mass \: [kg] \times g) \times radius \: [m]$$

Where:

$$g = 9.81 \: ms^{-2}$$ Equation 2

To Find a Gearmotor

Let’s say we want to lift a 0.7kg mass using a 4cm diameter pulley. We can find the torque load created by the mass using equation 2:

$$ \tau \: [Nm] = mass \: [kg] \times g \times radius$$

$$ = 0.7 \times 9.81 \times 0.02$$

$$= 0.137 Nm$$

$$= 137mNm$$

(Remeber that \(radius = \frac{diameter}{2}\) and \( 1mNm = 0.001 Nm\))

We need to find a gearmotor that can support at least this much torque. You can search through our selection of DC geared motors. So for our required torque, there are several motors which will be able to do the job, such as the 215-400 Micro Spur 16mm DC Gearmotor – 38mm type, which has a rated torque of 150mNm.

To Find a Pulley

Rearrange equation 2 for the radius, r:

$$r = \frac{\tau}{mass \times g}$$ Equation 3

Note that the minimum diameter of your pulley is limited by the shaft diameter of your motor. You might be able to bypass the pulley altogether, and simply super glue and wrap the string directly around the shaft.

It’s worth remembering that although a smaller pulley wheel means the motor will be able to lift a heavier weight, it will take longer to lift the mass. Our datasheets include a Typical Performance Characteristics Graph that shows the typical output speed at a range of torque loads.

If you’re concerned about efficiency, then you’ll want to run your motor at the rated voltage and rated torque – put these into equation 3 along with the mass of the object you’re lifting to figure out the radius you need to lift your mass.

How Much Can This Motor Lift?

Rearranging equation 2 for the mass we find:

$$mass_{max} = \frac{\tau _{stall}}{radius \times g}$$ Equation 4

For \(\tau\) you can use a figure close to the stall torque of the motor, which is found in the “Typical Mechanical Characteristics” of the datasheet. For the 215-400 we see it has a typical stall torque of 530mNm.

Note: that the typical stall torque only provides an estimate for the maximum weight, as it is the minimum load torque required to stall a spinning motor. The minimum load torque required to prevent a motor from starting is expected to be lower due to the inertia of the system – particularly true if a heavy pulley is used.

If you use equation 4 and the maximum mass the motor can lift turns out to be less than that you need, how about reducing the radius of the pulley? Or maybe choosing a motor with a greater torque?

Happy lifting!

---