AB-012
Driving Vibration Motors With Pulse Width Modulation
Overview
In previous Application Bulletins and in much vibration motor documentation, there are many references to Pulse Width Modulation (PWM) signals. This bulletin explains what a PWM signal is, the elements that it contains, its benefits for vibration motor control, and how it is commonly implemented in circuits.
PWM formulae are also provided to enable the user to estimate the results of a given PWM signal. In addition, graphs and example circuits are included to aid explanations. If you have any questions about PWM signals and their use with vibrating motors, you can contact us here.

Get in touch
Speak to a member of our team.
Motor catalogue
Looking for our products?
Reliable, cost-effective miniature mechanisms and motors that meet your application demands.
Pulse Width Modulation (PWM) Explained
A Pulse Width Modulated signal is a type of digital waveform. It alternates between bursts of ‘On’ and ‘Off’, also known as high and low respectively, at a fixed frequency. The PWM signal differs from other digital signals (e.g. square waves) because the time that the signal is high and low can be varied. This is useful because when the PWM signal is averaged with a simple analogue filter, a DC voltage is produced that is proportional to the duty cycle (which is the percentage of time that the PWM signal is high). Since a vibration motor’s speed and frequency of vibration is directly proportional to the voltage applied to the motor, we can use PWM to control precisely how the motor runs.
The specified frequency of the signal needs to be sufficiently high so that the load, in our case a vibration motor, does not see ‘bursts’ of high and low (the switching digital signal). Instead, we want the PWM signal to appear as a smooth averaged signal, which is proportional to the duty cycle of the digital signal.
Luckily, because of the inductive and resistive nature of a DC motor’s windings, it effectively has its own low pass analogue filter built in. If the load was purely resistive then the PWM waveform would still be visible. The example circuits below demonstrate the difference in the resulting voltage between an inductive load (with the motor) and a resistive load (without the motor). With the motor as a load, the PWM signal is clearly averaged (though still a little spiky/noisy, but we can improve on that later).
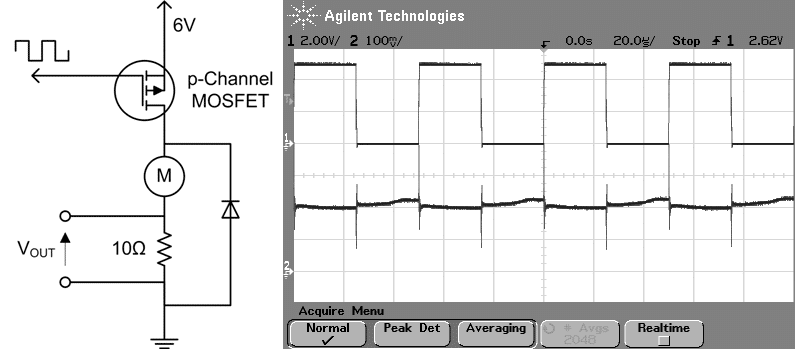
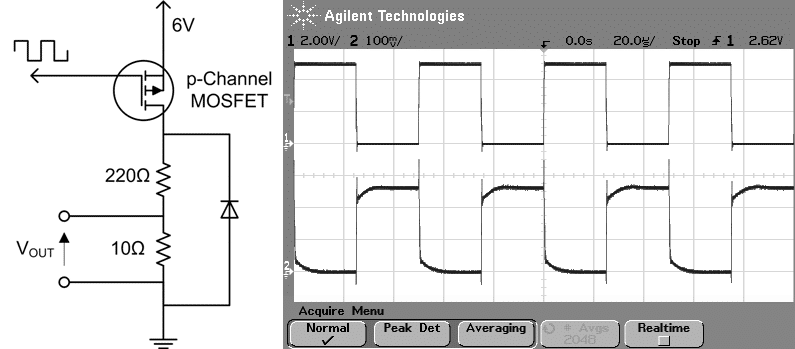
The width of the on burst can be adjusted by whatever is producing the PWM signal (typically a microcontroller), which is complemented by the inverse change in the off pulse width, thereby maintaining the same frequency. Changing the pulse widths results in a change of the average voltage after filtering, allowing any value between zero and the maximum voltage to be represented by increasing or decreasing the pulse width. Hence the term Pulse Width Modulation.
This enables analogue control of the motor using digital signalling, making it very useful in electronics systems that use microcontrollers to control the motor. Many microcontrollers have PWM generators built in, alternatively, the antique technique is to generate it using an analogue signal, a sawtooth signal, and a comparator.
Generating PWM signals is beyond the scope of this bulletin, instead, we will focus on how it can be used to drive the motor and assume that a suitable PWM source is readily available in the circuit.
The PWM signal has three separate components:
- A Voltage, 𝑉𝑃𝑊𝑀 – the value of the ‘on’ or high voltage level (typically between 2 ~ 5V if PWM signal is produced by a microcontroller / CMOS logic).
- A Frequency – the period of one clock cycle, i.e. one high pulse and one low pulse.
- A Duty Cycle – the ratio of the on-time to the off-time, which controls the resulting voltage, explained in detail below.
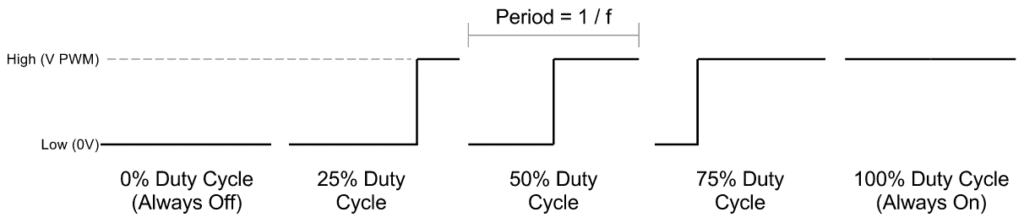
The Duty Cycle represents the length of the On pulse compared to one period cycle. It is expressed as a percentage. To illustrate the difference in Duty Cycles, there are example waveforms below:
The resulting voltage, which is seen by the motor, is the average voltage over the period. It is easily calculated using the following formula:𝑉𝐴𝑉𝐺=𝑉𝑃𝑊𝑀×𝐷𝑢𝑡𝑦𝐶𝑦𝑐𝑙𝑒
We can see from the formula that we can adjust the voltage by changing the Duty Cycle. For example, if we have a 3 V PWM signal with a 50% Duty Cycle, the average output voltage is:𝑉𝑂𝑈𝑇=𝑉𝐴𝑉𝐺=𝑉𝑃𝑊𝑀×𝐷𝑢𝑡𝑦𝐶𝑦𝑐𝑙𝑒𝑉𝑂𝑈𝑇=3𝑉×50𝑉𝑂𝑈𝑇=3𝑉×0.5𝑉𝑂𝑈𝑇=1.5𝑉
If we wanted to increase the voltage to 2.25V we can rearrange the formula to find the appropriate Duty Cycle:𝐷𝑢𝑡𝑦𝐶𝑦𝑐𝑙𝑒=𝑉𝑂𝑈𝑇𝑉𝑃𝑊𝑀𝐷𝑢𝑡𝑦𝐶𝑦𝑐𝑙𝑒=2.253𝐷𝑢𝑡𝑦𝐶𝑦𝑐𝑙𝑒=0.75𝐷𝑢𝑡𝑦𝐶𝑦𝑐𝑙𝑒=75
This means that controlling the speed of the motor, the vibration frequency and also the vibration strength, can easily be achieved by altering the PWM signal’s Duty Cycle in the microcontroller. The advantage of this technique is that the microcontroller can make a simple adjustment to its output depending upon the input conditions and its programme. Also, specific output waveforms can be stored in libraries or memory which can be recalled for certain events. This technique is used extensively for haptic feedback.
A Real-Life Example
Consider the simple waveform below:

Here we have a simple waveform which starts with a Duty Cycle of 25%, then increasing to 50%, and finally 75%. Note again that the maximum voltage and frequency have remained constant, and only the Duty Cycle has changed. We can calculate the average voltage over each section:
- 25% :: 𝑉𝑂𝑈𝑇=0.25×𝑉𝑃𝑊𝑀
- 50% :: 𝑉𝑂𝑈𝑇=0.50×𝑉𝑃𝑊𝑀
- 75% :: 𝑉𝑂𝑈𝑇=0.75×𝑉𝑃𝑊𝑀
The output voltage, which is the voltage seen by the motor, of the above waveform is shown below:
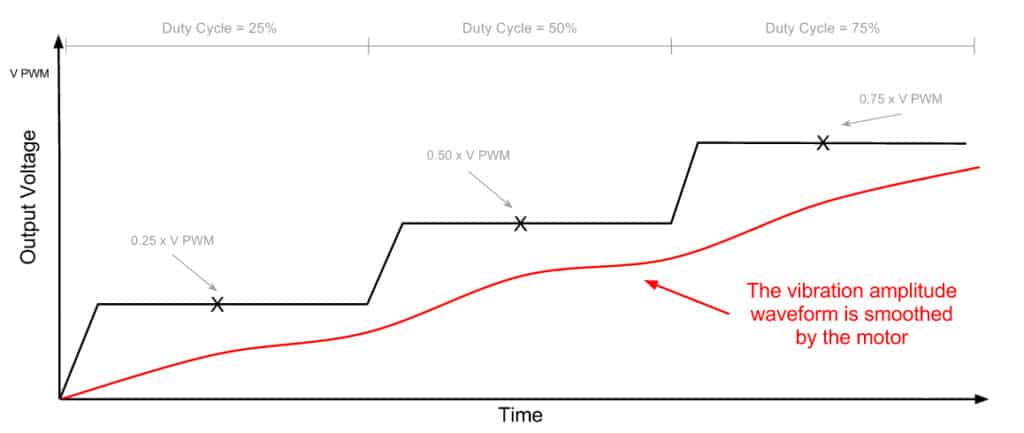
Please note this is an example aimed at demonstrating the effect of a change in the output voltage with differing the Duty Cycles and that the actual performance may differ. For instance, the acceleration between voltage levels can differ depending on the available current and other circuit components.
Driving Motors With PWM
As demonstrated above, a microcontroller can easily change the voltage applied to a motor using a PWM signal. It can build quite a complex waveform to increase haptic feedback performance and even store these waveforms in libraries or some remote memory location.
Unfortunately, it is not possible to drive the motor directly from the microcontroller itself due to the current draw of the motor. Hence a switching amplifier is needed which with appropriate PWM signals to tackle two issues:
- Supplying enough current to drive the motor.
- Supplying enough voltage to meet the required motor start voltage.
Microcontrollers are usually designed to be as efficient as possible with fast switching capabilities. As a result, they use low voltage and low current signals for their inputs and outputs. Vibration motors, as with most DC motors, have a Maximum Operating Current much higher than the microcontroller can provide.
In addition, ignoring the current supply problem, the DC output voltage from the microcontroller may also be too small. On our datasheets, we include the value Certified Start Voltage, which the voltage that the motor is guaranteed to start (in every orientation). Depending on the vibration motor and microcontroller choice, especially for our larger vibration motors, the Certified Start Voltage may be above the DC output voltage of the microcontroller.
As an example, we can compare a common microcontroller, the Atmel ATmega168 which is found on the popular Arduino Duemilanove development board, with our smallest vibration motor, the 303-100. The ATmega168 can provide DC currents of up to 40mA and voltages of 2.7V to 5V depending on the chip’s supply voltage.
The 303-100 has a Maximum Operating Current of 85mA (over double the ATmega168 maximum) and a Certified Start Voltage of 1.8V. Whilst the start voltage is sufficiently met in this case, the current is not.
If we assume a 2.7V supply voltage the range of PWM values at the start is reduced. A Duty Cycle of under 66% would reduce the average voltage below the motor’s start voltage.𝑀𝑖𝑛𝑖𝑚𝑢𝑚𝐷𝑢𝑡𝑦𝐶𝑦𝑐𝑙𝑒=𝑉𝑆𝑡𝑎𝑟𝑡𝑉𝑆𝑢𝑝𝑝𝑙𝑦𝑀𝑖𝑛𝑖𝑚𝑢𝑚𝐷𝑢𝑡𝑦𝐶𝑦𝑐𝑙𝑒=1.8𝑉2.7𝑉𝑀𝑖𝑛𝑖𝑚𝑢𝑚𝐷𝑢𝑡𝑦𝐶𝑦𝑐𝑙𝑒=0.66667𝑀𝑖𝑛𝑖𝑚𝑢𝑚𝐷𝑢𝑡𝑦𝐶𝑦𝑐𝑙𝑒=66.7
Once the motor is spinning, the user can utilise the full range of PWM values to vary the motor speed from low to high amplitudes. However, note that if the motor comes to rest due to too low a PWM signal, you will have to re-apply the start voltage to ensure that it will start spinning again in every instance.
To drive the motor we, therefore, need some additional circuitry to help fulfil the motors power requirements.
Amplifying The PWM Signal For Motors
This option is discussed fully in Application Bulletin 001: Discrete Driver Circuits for Vibration Motors. Here the PWM signal is used to switch a BJT or MOSFET, which in turn drives the motor from a higher power voltage source.
Example circuits of n-channel and p-channel MOSFETs are given below. While BJTs can be used instead of MOSFETs, they are generally less efficient and require additional thermal management. The PWM signal should have a high enough voltage such that the MOSFET is operating in the saturation region, otherwise, it too will require a heat-sink, and be very inefficient. To achieve saturation, try to select a MOSFET with a Vgs that is less than 1/3rd of the Vmax of the PWM signal; this will ensure the MOSFET is switched hard on. The pull-down resistor will ensure that it’s switched hard-off.
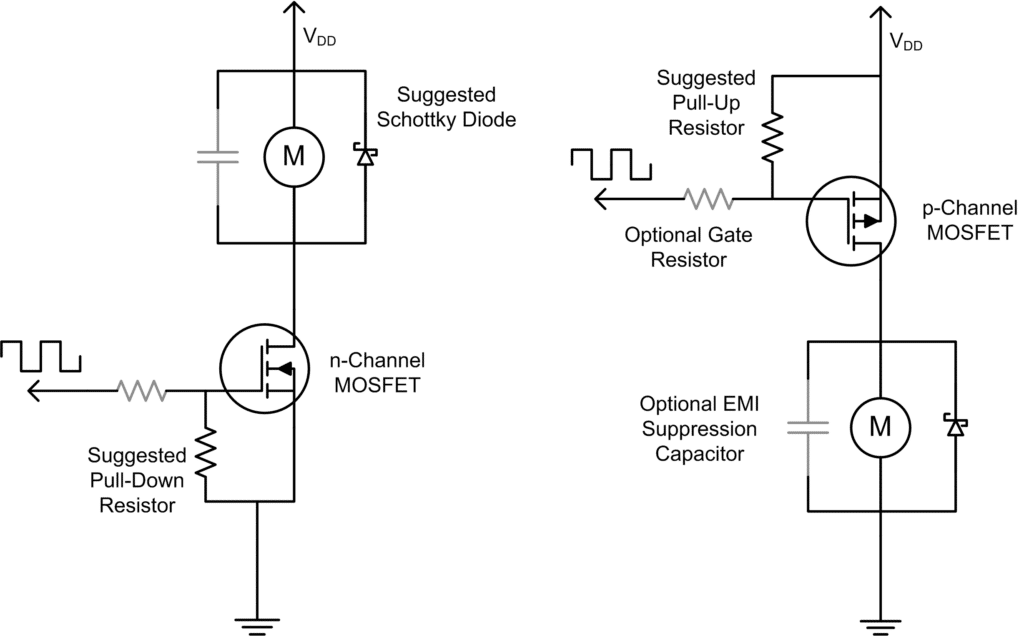
The motor’s supply voltage is now a factor of 𝑉𝐷𝐷, which should be able to provide a high enough voltage and current to adequately drive the motor. The effect of the Duty Cycle remains the same, except 𝑉𝑃𝑊𝑀 is replaced by 𝑉𝐷𝐷.𝑉𝑚𝑜𝑡𝑜𝑟=𝑉𝐷𝐷×𝐷𝑢𝑡𝑦𝐶𝑦𝑐𝑙𝑒
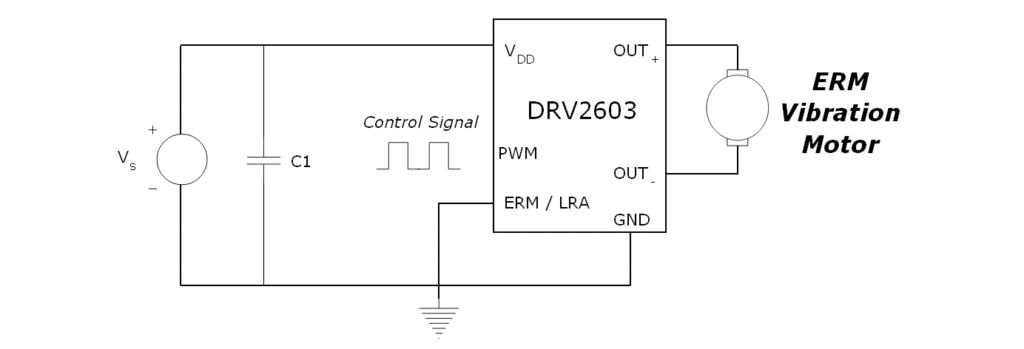
Using A Motor Drive IC
Motor drive chips have multiple benefits. They can have built-in H-bridges for advanced driving techniques, help with voltage regulation, and often accept PWM signals as a control. See Application Bulletin 023: Miniature Motor Driver Resource for a list of suggested drivers for different applications.
For more information on how H-Bridges can benefit haptic feedback performance, see Application Bulletin 002: Discrete H-bridge circuits for enhanced vibration motor control. We have also published an Application Bulletin on chips for driving Linear Resonant Actuator vibration motors, and although LRAs have different requirements to eccentric rotating mass vibration motor’s some of the integrated circuits reviewed can be used to drive both vibration motor types. See AB-003: How to Drive Linear Resonant Actuators for more information.
Many motor drive ICs can accept a PWM signal and adjust their output accordingly. More information will be available in the specific chip’s datasheet.
Using a PWM signal with a chip that includes H-bridge control can enable the user to easily implement advanced haptic techniques such as overdrive and reverse braking. To quickly start the vibration motor, it can be supplied with a voltage above its rated voltage for a short period of time. This is known as ‘overdriving’ the motor. Conversely, to quickly stop the motor the polarity of the voltage can be inverted, essentially driving the motor against its current direction of rotation. This is known as reverse braking.
Some motor drive ICs will be able to support the above techniques and use the PWM signal’s Duty Cycle to determine its output, for example, the following setup may be achieved:
| PWM Duty Cycle | Output |
| 100% | Overdrive Clockwise |
| 90% | Rated Voltage Applied Clockwise |
| 50% | No Rotation |
| 10% | Rated Voltage Applied Counter-Clockwise |
| 0% | Overdrive Counter-Clockwise |
Selecting PWM Frequencies And EMI / Noise Suppression
In our previous Application Bulletin 005 Electromagnetic Compatibility (EMC / EMI) with Vibration Motors we looked at methods for reducing electromagnetic interference, or EMI.
A common technique for minimising EMI is to use a capacitor as close to the motor terminals as possible. This filters out high-frequency noise, and unfortunately, this can also filter PWM signals. To avoid this, the value of the capacitor must be chosen so the resonant frequency of the system is far from that of the PWM. The frequency of the PWM signal is usually around 20 kHz or higher, and a 10 – 100 pF capacitor would suffice.
The resonant frequency 𝑓𝑟 can be calculated as:𝑓𝑟=12𝜋𝐿𝑚𝐶𝑒‾‾‾‾‾‾√
Where 𝐿𝑚 is the motor inductance and 𝐶𝑒 is the external decoupling capacitor. For motors with low terminal resistance, an additional resistor in series with the capacitor will help with the dumping.
A more comprehensive solution involves two additional capacitors to the one above, one per motor terminal, connected between the terminal and motor housing. This will reduce the arcing, especially for carbon brush motors.
Conclusion
Using a PWM signal to drive vibration motors can enable high-performance vibration control with relative ease. PWM signals are a common feature in many microcontrollers, and simple programs can adjust their frequency and Duty Cycle. These programs can be used to create complex PWM waveforms, and store them for later use.
The Duty Cycle of the PWM signal represents the length of the On pulse in one wave cycle, expressed as a percentage. This alteration of the width of the pulse affects the average voltage. When a PWM signal, which has a high frequency, is applied to a DC or vibration motor then it is the average voltage that drives the motor. This allows users to control the speed of the motor, or strength of vibration, by adjusting the Duty Cycle.
Typical microcontrollers cannot provide enough current, and in some cases voltage, to drive a vibrating motor. It is therefore recommended that they be used in conjunction with drive circuitry, examples of which are provided in the appropriate sections and more information can be found in other motor application notes.
Newsletter
Sign up to receive new blogs, case studies and resources – directly to your inbox.

Sign up
Discover more
Resources and guides
Discover our product application notes, design guides, news and case studies.
Case studies
Explore our collection of case studies, examples of our products in a range of applications.
Precision Microdrives
Whether you need a motor component, or a fully validated and tested complex mechanism – we’re here to help. Find out more about our company.