AB-024
Introductory Gear Equations
There are a couple of ways to get the exact speed you need on a motor, although we’d like to think that we provide a fairly comprehensive range of gear motors. If you can’t find an off-the-shelf solution, we’re always happy to help discuss custom variations or encoder / PID solutions with you – just drop our engineers a line.
For quickly experimenting or prototyping, you may wish to build your own cheap gear chain. Here we’ll take a look at a couple of basic calculations to get you started and which should provide an easy reference to return to as you need.
Relationship Between Two Gears
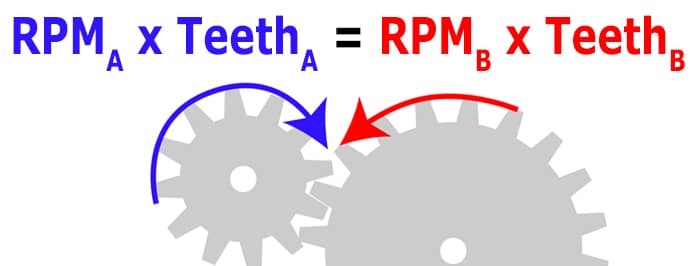
When two gears are connected (we say ‘in mesh’) the speed relationship is very simple and is dependent only on the number of teeth in each gear. That is, the ratio of teeth is equal to the inverse ratio of speed. It is easier to understand when written as an equation:𝑇𝑒𝑒𝑡ℎ𝐴𝑇𝑒𝑒𝑡ℎ𝐵=𝑅𝑃𝑀𝐵𝑅𝑃𝑀𝐴
Or you may find it easier to remember that the product of the number of teeth and speed equal between the gears, i.e. the number of teeth times the speed of gear A will equal the number of teeth times the speed of gear B:𝑅𝑃𝑀𝐴×𝑇𝑒𝑒𝑡ℎ𝐴=𝑅𝑃𝑀𝐵×𝑇𝑒𝑒𝑡ℎ𝐵
Whichever way is easier for you to remember, we can calculate any one variable assuming we have the other three. Often, we may already have a motor and desired output speed – using the first equation we can find the required ratio of teeth on the gears.

Get in touch
Speak to a member of our team.
Motor catalogue
Looking for our products?
Reliable, cost-effective miniature mechanisms and motors that meet your application demands.
For example, our 108-106 has a no load speed of 18,000 RPM at 3V. Let’s say we wanted to reduce this to under 5,000 RPM:𝑇𝑒𝑒𝑡ℎ𝐴𝑇𝑒𝑒𝑡ℎ𝐵=𝑅𝑃𝑀𝐵𝑅𝑃𝑀𝐴𝑇𝑒𝑒𝑡ℎ𝐴𝑇𝑒𝑒𝑡ℎ𝐵=5,000𝑅𝑃𝑀18,000𝑅𝑃𝑀𝑇𝑒𝑒𝑡ℎ𝐴𝑇𝑒𝑒𝑡ℎ𝐵=0.277778
OR𝑇𝑒𝑒𝑡ℎ𝐵𝑇𝑒𝑒𝑡ℎ𝐴=3.6
This means our second gear needs to have at least 3.6 times as many teeth as our first gear. If gear A has 10 teeth, gear B must have at least 36. You may have to compromise when it comes to gear selection, not every value of teeth is available and you may find even numbers more common than odd.
A quick delve into a handful of our office supply returns the following sizes:
- 60 teeth
- 42 teeth
- 30 teeth
- 16 teeth

Using the 16 tooth size as gear A and the 60 tooth size as gear B gives us a ratio of 3.75 between the gears. This equates to 4,800 RPM when used with the 108-106. Note that due to the nature of the way the gears mesh, they will turn in opposite directions.

If we needed to reduce the output speed even further, say close to 1,000 RPM, we would need to increase the gearing ratio – but how do we overcome size restrictions? Most applications are limited in space, and the more teeth you require the greater the diameter of the gear.
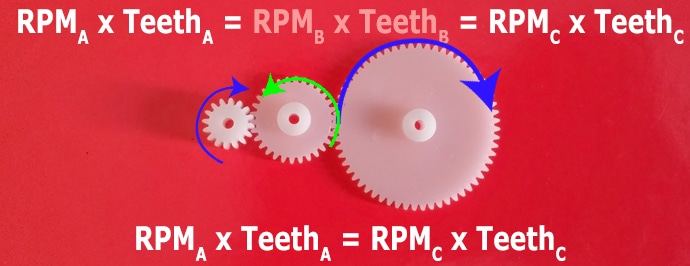
Adding In Gears
Your first instinct may be to simply add a third gear, but as we will see that this has no effect on the output speed. Remember when two gears are in mesh:𝑅𝑃𝑀𝐴×𝑇𝑒𝑒𝑡ℎ𝐴=𝑅𝑃𝑀𝐵×𝑇𝑒𝑒𝑡ℎ𝐵
So the relationship between our third and second gear is given as:𝑅𝑃𝑀𝐵×𝑇𝑒𝑒𝑡ℎ𝐵=𝑅𝑃𝑀𝐶×𝑇𝑒𝑒𝑡ℎ𝐶
Therefore:𝑅𝑃𝑀𝐴×𝑇𝑒𝑒𝑡ℎ𝐴=𝑅𝑃𝑀𝐵×𝑇𝑒𝑒𝑡ℎ𝐵=𝑅𝑃𝑀𝐶×𝑇𝑒𝑒𝑡ℎ𝐶𝑅𝑃𝑀𝐴×𝑇𝑒𝑒𝑡ℎ𝐴=𝑅𝑃𝑀𝐶×𝑇𝑒𝑒𝑡ℎ𝐶𝑇𝑒𝑒𝑡ℎ𝐴𝑇𝑒𝑒𝑡ℎ𝐶=𝑅𝑃𝑀𝐶𝑅𝑃𝑀𝐴
The relationship between the speed of the input and the speed of the output is only dependant upon the ratio of teeth between the input and the output gears. However, the addition of the second gear does ensure the input and output gears turn in the same direction.
Compound Gears
This is overcome by using what is known as a compound gear, where a single gear has two different sets of teeth:

With the compound gear the speed is preserved between the gear’s two sets of teeth. Using a compound gear, lets look at how our speed and teeth relationship is changed. To explain, we will treat the compound gear as two separate gears (B and C) that are forced to the same speed. We now have two separate meshes:𝑅𝑃𝑀𝐴×𝑇𝑒𝑒𝑡ℎ𝐴=𝑅𝑃𝑀𝐵×𝑇𝑒𝑒𝑡ℎ𝐵
and𝑅𝑃𝑀𝐶×𝑇𝑒𝑒𝑡ℎ𝐶=𝑅𝑃𝑀𝐷×𝑇𝑒𝑒𝑡ℎ𝐷
However the speeds of gear B and gear C are equal, we’ll rename it 𝑅𝑃𝑀𝐵𝐶 to clarify:𝑅𝑃𝑀𝐴×𝑇𝑒𝑒𝑡ℎ𝐴=𝑅𝑃𝑀𝐵𝐶×𝑇𝑒𝑒𝑡ℎ𝐵𝑅𝑃𝑀𝐵𝐶×𝑇𝑒𝑒𝑡ℎ𝐶=𝑅𝑃𝑀𝐷×𝑇𝑒𝑒𝑡ℎ𝐷
We can rearrange each equation to give a value for 𝑅𝑃𝑀𝐵𝐶:𝑅𝑃𝑀𝐵𝐶=𝑅𝑃𝑀𝐴×𝑇𝑒𝑒𝑡ℎ𝐴𝑇𝑒𝑒𝑡ℎ𝐵𝑅𝑃𝑀𝐵𝐶=𝑅𝑃𝑀𝐷×𝑇𝑒𝑒𝑡ℎ𝐷𝑇𝑒𝑒𝑡ℎ𝐶𝑅𝑃𝑀𝐷×𝑇𝑒𝑒𝑡ℎ𝐷𝑇𝑒𝑒𝑡ℎ𝐶=𝑅𝑃𝑀𝐴×𝑇𝑒𝑒𝑡ℎ𝐴𝑇𝑒𝑒𝑡ℎ𝐵
Our output speed is therefore:𝑅𝑃𝑀𝐷=𝑅𝑃𝑀𝐴×𝑇𝑒𝑒𝑡ℎ𝐴×𝑇𝑒𝑒𝑡ℎ𝐶𝑇𝑒𝑒𝑡ℎ𝐵×𝑇𝑒𝑒𝑡ℎ𝐷
Teeth A and C can be thought of as transmitting power, i.e. these are forcing teeth B and D to rotate. You can think of the output speed as the input speed times the product of transmitting teeth divided by the product of receiving teeth:𝑂𝑢𝑡𝑝𝑢𝑡𝑆𝑝𝑒𝑒𝑑=𝐼𝑛𝑝𝑢𝑡𝑆𝑝𝑒𝑒𝑑×𝑃𝑟𝑜𝑑𝑢𝑐𝑡𝑜𝑓𝑇𝑟𝑎𝑛𝑠𝑚𝑖𝑡𝑡𝑖𝑛𝑔𝑇𝑒𝑒𝑡ℎ𝑃𝑟𝑜𝑑𝑢𝑐𝑡𝑜𝑓𝑅𝑒𝑐𝑒𝑖𝑣𝑖𝑛𝑔𝑇𝑒𝑒𝑡ℎ

Back to our example, it just so happens the 42 tooth gear happens to be a compound gear with a 10 tooth secondary gear. We’ll continue to use the smallest gear to drive and the biggest as the final stage to maximise our overall gearing. So our setup now looks as follows:
- Gear A: 16 teeth
- Gear B: 42 teeth (compound with Gear C)
- Gear C: 10 teeth (compound with Gear B)
- Gear D: 60 teeth
Still using the 108-106 at 18,000 RPM, what would we expect the new output speed to be?𝑅𝑃𝑀𝐷=𝑅𝑃𝑀𝐴×𝑇𝑒𝑒𝑡ℎ𝐴×𝑇𝑒𝑒𝑡ℎ𝐶𝑇𝑒𝑒𝑡ℎ𝐵×𝑇𝑒𝑒𝑡ℎ𝐷𝑅𝑃𝑀𝐷=18,000×16×1042×60𝑅𝑃𝑀𝐷=1,143𝑅𝑃𝑀
Still a little above our target, but we’ve reduced the the output speed by ~94% – which is a significant reduction from only a few gears!

Once we understand how the speed is reduced through the gear chain, calculating the transfer of torque is simple: it is the inverse of the speed ratio.
As the output speed of the gear chain decreases, the system can deliver more torque. If you browse our product catalogue, you can see that for similar motors (for example our 212-4XX) as the Gear Ratio increases, the Rated Torque increases, and the Rated Speed decreases.
An important note is to remember that the speed depends on the level of required torque. So a motor’s output speed is always at a specified level of torque. The Rated Speed is at the Rated Torque, and other values can be read from the Typical Performance characteristics graphs.
If the load is constant, a better way of thinking about it is not to consider the torque as an output of the motor but as an input to the system. With our known load at the output gear, we actually work backwards to find what load motor is seen by the motor. From there we can read the Typical Performance Characteristics and estimate the speed of the motor and other details such as the current draw.
Alternatively, if you want to calculate the maximum torque a motor can deliver with its new gear chain, you would take the Stall Torque value from the motor’s datasheet and use the relationship below to calculate the output torque. This is useful if you don’t care about speed, you just want to make sure the load is moved (or have a wide tolerance for your speed).
There are a few caveats with this, first at stall the speed is obviously 0 RPM – but using a ‘close to stall’ speed of 1 RPM avoids divisions/multiplications by zero. Secondly, sometimes stall torques are estimates – a motor doesn’t always steadily decrease to 0 RPM so it would be wise to use a margin of error. Lastly, once a motor is running it can handle a greater torque load than when it’s first starting to turn. That means the Stall Torque is likely to be a greater value than the maximum starting torque.
We’ll consider each of these scenarios, but first, let’s review the relationship. For two gears in mesh, we’re essentially replacing the Teeth with the Torque (pull the teeth out!):
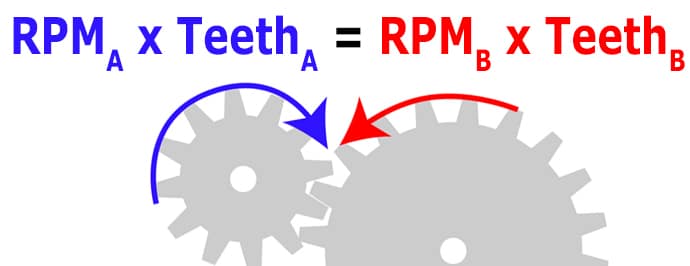
𝑇𝐴𝑇𝐵=𝑅𝑃𝑀𝐵𝑅𝑃𝑀𝐴
or𝑅𝑃𝑀𝐴×𝑇𝐴=𝑅𝑃𝑀𝐵×𝑇𝐵
For a more complicated compound gear chain it will likely be easiest to first calculate the speed ratio using the teeth of the gears, then invert it for the torque ratio. Alternatively:𝑇𝐷=𝑇𝐴×𝑇𝑒𝑒𝑡ℎ𝐵×𝑇𝑒𝑒𝑡ℎ𝐷𝑇𝑒𝑒𝑡ℎ𝐴×𝑇𝑒𝑒𝑡ℎ𝐶

In this case, 𝑇𝐴 would be the stall torque of the motor and 𝑇𝐷 would be the maximum load on the output gear.
A Worked Example
Let’s go through a worked example, say we have a known load of 2.5 mNm, the 108-106, and the gear chain above. We want to figure out how fast the load will move, we can calculate it in the following steps:
- Calculate the gearing ratio
- Calculate the torque seen by the motor
- Read the Typical Performance Characteristics to see 108-106’s speed at that torque
- Use the gear ratio to determine the speed at the load
Using the same gear chain as above, we calculate the ratio for the torque:
Using the same gear chain as above, we calculate the ratio for the torque:𝑇𝐷=𝑇𝐴×𝑇𝑒𝑒𝑡ℎ𝐵×𝑇𝑒𝑒𝑡ℎ𝐷𝑇𝑒𝑒𝑡ℎ𝐴×𝑇𝑒𝑒𝑡ℎ𝐶𝑇𝐷=𝑇𝐴×42×6016×10𝑇𝐷=𝑇𝐴×15.75
Now, we know the load 𝑇𝐷 is 2.5 mNm, which means the torque seen by the motor is:𝑇𝐴=𝑇𝐷15.75𝑇𝐴=2.515.75𝑇𝐴=0.159𝑚𝑁𝑚
Reading the 108-106 datasheet, we would expect the motor to turn at (roughly) 14,000 RPM and draw 140 mA. With the motor’s speed known, we can use the gear ratio to calculate the output speed:𝑅𝑃𝑀𝐷=𝑅𝑃𝑀𝐴15.75𝑅𝑃𝑀𝐷=14,00015.75𝑅𝑃𝑀𝐷=889𝑅𝑃𝑀
A small caveat is all calculations we have ignored the friction and inertia present in the gear chain at rest (which would be very small for these plastic gears, but not for large metal gears).
Newsletter
Sign up to receive new blogs, case studies and resources – directly to your inbox.

Sign up
Discover more
Resources and guides
Discover our product application notes, design guides, news and case studies.
Case studies
Explore our collection of case studies, examples of our products in a range of applications.
Precision Microdrives
Whether you need a motor component, or a fully validated and tested complex mechanism – we’re here to help. Find out more about our company.